你可能还不够了解的数据结构 — 堆 (Heap)

初学数据结构的时候我们可能都觉得它很枯燥，既看不懂它是咋实现的，也不知道它究竟有啥用，就知道这个面试要考，所以我要会。其实，随着我们编码年龄的增长，我们就会越来越觉得数据结构真的是可堪大用，能熟练应用数据结构也是一个计算机工程师能力的试金石，这也解释了它为什么在任何级别的工程师面试中都未曾缺席过。今天我们就来聊一聊一个非常重要的数据结构 – 堆（Heap），之所以选择了它是因为在很多初学的小伙伴眼里，它好像很神秘很复杂的样子，但其实他并不比我们熟知的二叉树、单链表更加高贵，今天我们就来一起揭开它的面纱。

什么是Heap？

• 形状：它是计算机科学中的一种特别的树状结构
• 分类：基本可以分为最大堆（max heap）和最小堆（min heap）两种（以下我们均以最小堆为例）
• 定义：任意结点P和C，若P是C的父结点，则P的值一定小于等于C的值。

重要结论：

1. 根节点的值一定是最小的（或之一）
2. 父结点的值必然小于等于它的任何一个子结点
3. 同层节点之间没有必然的大小关系

堆就是树的一种吗？

我们常用的堆是二叉堆（binary heap）也就是基于二叉树结构实现的堆，但是请注意，堆不是一定是二叉树哦，所以我们只是常用“堆”来代指“二叉堆”，在这里我们也会继续沿用这一种叫法。堆是一种特殊的二叉树，它必须是完全二叉树（complete tree），也就是说如果你将一颗二叉树按照从上到下从左到右的顺序依次从1开始编号，编号序列是连续自然数而中间没有空缺。

这颗树是一个正确的最小堆吗？ 

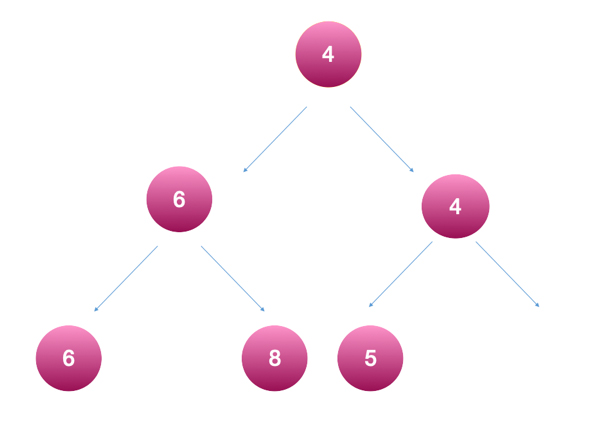
是的。请再看一遍上面的定义和结论哦。

为什么需要这个数据结构？

对于每一个新的数据结构，我们都需要搞清楚为什么需要它，这是我们能够记住并且使用它的关键。而理解数据结构存在意义的关键，就是要清楚它的出现使什么问题变得简单了？这个问题就是对于任何一个数字集合，我们如何知道并且尽可能快速地知道他的最（小）值。你可能会说我们可以将它进行排序吧，但是如果我们完全不关心除了最（小）值意外的任何数据之间的大小关系呢？排序是不是就做了太多不必要的工作。而且如果这是一个随时面临被更新的集合呢？我们怎么随时知道这个集合最新的最（小）值呢？再向前推进一步，如果它被任意划分为若干个子集的时候，我们能否依然知道这些再次被划分出来的子集的最（小）值呢？因而我们就思考去让这个数据结构拥有一个性质去保持最（小）值在一个特殊点，而它的每一个子结构也保持同样的性质。因而我们就自然的选择了树型结构，而这个特殊点就是根节点，而每一个节点又恰恰是它所在子树的根节点。

如何插入一个节点？

由于需要维持完全二叉树的结构，我们需要先将新节点插入最底层的最右边，然后逐层与它的父节点比较，如果它的值比父节点的值小（最小堆为例），交换两个节点，也叫“节点上浮”：

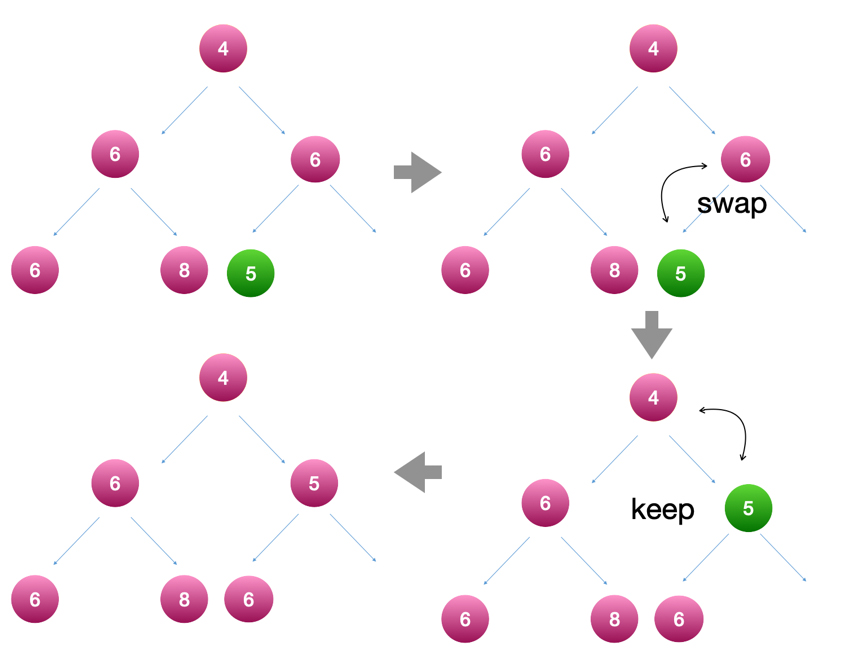
所以我们可以观察到，最坏的情况是我们插入了一个最小的点，然后将它一路“上浮”到跟节点，走过的路径就是二叉树的高度，如果我们用N代表节点总数，它的时间复杂度就是O(logN)。

如何删除一个节点？

学习数据结构和算法的一个重要方法就是模仿已知的方法去解决新问题，你能否应用插入时候使用的思想解决删除节点的问题呢？例如我们要删除上面结构中第二层左边的6该怎样做？提示：同样利用完全二叉树的末尾点。

堆是用什么实现的呢？

用JAVA的同学应该知道，在JAVA中并没有叫heap的结构，而是使用PriorityQueue实现了heap。同样的在python中对应的module叫做heapq。那么这是不是意味着heap其实是通过queue实现的呢？答案是可以，但不是最好。我们知道越底层越基础的数据结构的使用开销是越小的，所以heap在很多语言里都是用数组实现的，而且不要觉得这是一项多么难的工程，我们经过简单的学习也能轻而易举地用array实现自己的heap结构。

为什么必须是完全二叉树？

其实堆不一定是完全二叉树，我们平常使用的堆是基于它的一个经典的完全二叉树实现，而这样的结构被广泛使用是因为它便于存储和索引。想想一下我们如果需要给一个二叉树的每一个节点编号，什么方法是最符合人类习惯的？逐层从上到下从左到右吧。这样对于一个编号为i的节点，它的左子节点编号就是2*i, 而又子节点就是2*i + 1。而完全二叉树恰恰就是我们在满二叉树删掉一些节点之后，使用同样的逐层编号的方式不会导致其他节点的编号发生变化。显而易见的是，删除的就是叶子节点中靠右的部分。所以我们不必为了保持编号的性质去定义一些空的节点，同时还能保持它的层数一直是logN，索引起来不会面临路径过长的问题。而且我们在删除节点的时候也很容易保持其性质，把最右叶子拿来填补被删除节点即可。

怎样初始化一个堆结构？

既然我们可以用数组实现堆结构，那么我们最初是怎么把一个数组初始化成一个堆结构的呢？聪明的小伙伴可能已经想到了，很简单，把每个元素以此插入这个堆不就行了么？当然，这个方法叫做“插入法”，假设我们一共有N个元素，每次插入的时间复杂度是logN, 所以初始化这个堆的总时间复杂度就是O(NlogN)。但是你知道这并不是最好的方法吗？其实我们可以用平均O(N)的时间进行高效的heapify操作。

为什么我经常听到别人说“堆栈”？为什么堆（heap）和栈（stack）能相提并论呢？

其实这是一个专业用语的问题，堆（heap）和栈（stack）有两个含义，一个是指抽象数据结构，另一个是指操作系统中的内存空间。前者它们实现和作用都有很大差异所以比较少被放在一起比较，后者则是同气连枝常常被“相提并论”。堆在操作系统中为按需申请、动态分配，由于内存中的空闲空间不是连续的，操作系统会根据应用程序提出的申请从堆中按照一定的算法找出可用内存标记后给程序使用；而操作系统中的栈则是程序运行时自动拥有的一小块内存，大小由编译器参数决定，用于局存放局部变量或者函数调用栈的保存。它们的区别如果长篇大论会讲非常多的内容，简单总结起来就是：

• 堆： 时效持久、全局可见、手动申请、手动释放
• 栈：时效临时、局部可见、自动申请、自动释放

其实关于堆还有很多有意思的东西值得探讨，然而由于篇幅有限，我们今天就暂时讨论到这里吧。